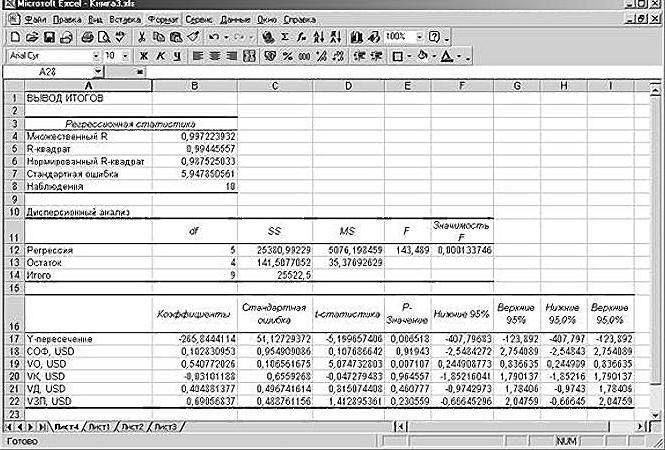
Lineární regrese

Regresní analýza může býtstatistické metody zkoumání vztahu mezi určitými proměnnými (závislé a nezávislé). V tomto případě se nezávislé proměnné nazývají "regresory" a závislé proměnné jsou "kritické". Při provádění lineární regresní analýzy je reprezentace závislé proměnné provedena ve formě intervalové stupnice. Existuje možnost nelineárních vztahů mezi proměnnými souvisejícími s intervalovou stupnicí, ale tento problém je již řešen metodami nelineární regrese, což není téma tohoto článku.

Lineární regrese se poměrně úspěšně používá jak v matematických výpočtech, tak v ekonomických studiích založených na statistických údajích.

Takže tuto regresi zvažte podrobněji. Z hlediska matematické metody určování lineárního vztahu mezi některými proměnnými může být lineární regrese reprezentována ve tvaru následujícího vzorce: y = a + bx. Dekódování tohoto vzorce lze nalézt v jakékoli učebnici o ekonometrii.

Při rozšíření počtu pozorování (až nkrát) se získá jednoduchá lineární regrese reprezentovaná vzorem:

yi = A + bxi + ei,

kde ei jsou nezávislé náhodně distribuované náhodné proměnné.

V tomto článku bych chtěl více pozornostidávají tento koncept z pohledu předikce budoucích cen na základě předchozích údajů. V této oblasti výpočtu lineární regrese aktivně využívá metodu nejmenších čtverců, která pomáhá vytvářet "nejvhodnější" přímku přes určitou sérii bodů cenových hodnot. Jako vstupní data se používají cenové body, které označují maximální, minimální, uzavírací nebo otevírací hodnotu, stejně jako průměrné hodnoty z těchto hodnot (například součet maxima a minima rozdělených na dvě). Tato data mohou být také libovolně vyhlazena před vytvořením vhodné linky.

Jak bylo uvedeno výše, lineární regresepoměrně často používaný v analytice k určení trendu na základě cenových a časových dat. V tomto případě indikátor regresního svahu umožní určit velikost změn cen za jednotku času. Jednou z podmínek pro správné rozhodnutí při použití tohoto indikátoru je použití signálů ve formě generátoru po trendu regresního svahu. Je-li sklon kladný (zvyšující se lineární regrese), nákup se provede, pokud je hodnota indikátoru větší než nula. Během negativního náklonu (klesající regrese) by se prodej měl uskutečnit s negativními hodnotami indikátoru (méně než nula).

Používá se při určování nejlepšího řádku odpovídající určitému počtu cenových bodů, metoda nejmenších čtverců zahrnuje následující algoritmus:

- je celková vyjádření čtverců cenového rozdílu a regresní linie;

- je poměr přijaté sumy a počtu sloupců v rozsahu regresních datových řad;

- z dosaženého výsledku se vypočte druhá odmocnina, která odpovídá standardní odchylce.

Rovnice párové lineární regrese má tento model:

y (x) = f ^ (x),

kde y je výsledný atribut reprezentovaný závislou proměnnou;

x je vysvětlující nebo nezávislá proměnná;

^ ukazuje absenci přísného funkčního vztahu mezi proměnnými x a y. Proto v každém jednotlivém případě může být proměnná y složena z těchto výrazů:

y = yx + ε,

kde y je skutečné výsledky;

yx - teoretická data výsledku určená řešením regresní rovnice;