Kinematika materiálu: základní pojmy, prvky

Tématem dnešního článku bude kinematikamateriální bod. Co to je? Jaké pojmy jsou v něm zahrnuty a jaká definice je nezbytná k tomu, aby tento termín? Na tyto a mnohé další otázky se budeme snažit.

Definice a koncepce

Kinematika materiálu jenic víc než podsekce fyziky nazývané "mechanika". Na druhou stranu studuje vzory pohybů některých těl. Kinematika hmotného bodu se také zabývá tímto úkolem, ale nedělá to obecným způsobem. Tato podkapitola ve skutečnosti zkoumá metody, které nám umožňují popsat pohyb těles. V tomto případě jsou pro vyšetřování vhodné pouze tzv. Idealizované orgány. Patří sem: materiálový bod, naprosto pevné tělo a ideální plyn. Zvažte koncepce podrobněji. Všichni víme ze školní lavice, že materiálním bodem je tělo, jehož rozměry lze v této nebo té situaci zanedbávat. Mimochodem kinematika translačního pohybu hmotného bodu se poprvé objevuje v učebnicích sedmé třídy ve fyzice. Jedná se o nejjednodušší odvětví, a proto je nejvhodnější začít s vědomím vědy s jeho pomocí. Samostatným problémem jsou prvky kinematiky hmotného bodu. Existuje mnoho z nich a podmíněně je lze rozdělit na několik úrovní, které mají různou složitost pro pochopení. Pokud například mluvíme o radiusovém vektoru, pak v zásadě neexistuje nic mimořádně složitého ve své definici. Souhlasíte však s tím, že pro něj bude mnohem jednodušší pochopit ho než studenta na střední nebo střední škole. A abych byl upřímný, není třeba vysvětlovat zvláštnosti tohoto termínu studentům středních škol.

Stručná historie tvorby kinematiky

Mnoho, před mnoha lety, velkým vědcemAristotle věnoval lvu podíl svého volného času studiu a popisu fyziky jako samostatné vědy. Konkrétně pracoval na kinematiku a snažil se prezentovat své hlavní teze a koncepty, které se používají při řešení konkrétních a dokonce běžných úkolů. Aristotle dal počáteční představu o tom, jaké jsou prvky kinematiky hmotného bodu. Jeho díla a práce jsou velmi cenné pro celé lidstvo. Nicméně ve svých závěrech udělal značné množství chyb a byl způsoben určitými chybami a chybnými výpočty. Práce Aristotla najednou měla zájem o jiného vědce - Galileo Galilei. Jednou ze základních tezí předložených Aristotelem bylo, že pohyb těla nastane, pouze pokud působí na nějakou sílu, určenou intenzitou a směrem. Galileo prokázal, že je to chyba. Síla bude mít vliv na parametr rychlosti, ale ne více. Italština ukázala, že síla je příčinou zrychlení a může se objevit pouze ve vzájemnosti. Také Galileo Galileo věnoval značnou pozornost studiím procesu volného pádu, odvozování odpovídajících vzorů. Pravděpodobně si každý pamatuje své slavné experimenty, které strávil na Šikmé věži v Pise. Ve svých dílech byl základ kinematických řešení používán fyzikem Ampere.

Počáteční koncepce

Jak již bylo uvedeno výše, metody kinematografických studiípopis pohybu idealizovaných objektů. V tomto případě lze v praxi uplatnit základy matematické analýzy, obyčejné algebry a geometrie. Ale jaké jsou koncepty (pojmy, ne definice a parametrické hodnoty), které jsou základem této subsekce fyziky? Za prvé, každý musí jasně pochopit, že kinematika translačního pohybu hmotného bodu považuje pohyb bez ohledu na silové ukazatele. To znamená, že k řešení odpovídajících problémů nepotřebujeme vzorce vztahující se k síle. Nezohledňuje kinematiku, bez ohledu na to, kolik z nich - jeden, dva, tři, alespoň několik set tisíc. Nicméně existuje ještě zrychlení. V řadě problémů určuje kinematika pohybu hmotného bodu určení velikosti zrychlení. Důvody tohoto jevu (tj. Síly a jejich povaha) však nejsou zohledněny, ale jsou vynechány.

Klasifikace

Zjistili jsme, že kinematika zkoumá a aplikujeMetody popisu pohybu těles bez ohledu na síly působící na ně. Mimochodem, tento úkol je již zpracován jinou podsekcí mechaniky, která se nazývá dynamika. Newtonovy zákony jsou již uplatněny, což umožňuje určit v praxi spoustu parametrů s malým počtem známých počátečních dat. Základní pojmy kinematiky hmotného bodu jsou prostor a čas. A v souvislosti s vývojem vědy obecně a v této oblasti vznikla otázka, zda je vhodná kombinace.

Od samého začátku bylo klasickékinematika. Lze říci, že není jenom přítomnost jak časových, tak prostorových rozdílů, které jsou pro ni zvláštní, ale také jejich nezávislost na volbě tohoto nebo toho referenčního rámce. Mimochodem, o tom budeme později promluvit. Nyní jen vysvětlete, co je v sázce. Interval mezery v tomto případě bude považován za segment, časový interval je časový interval. Zdá se, že všechno musí být jasné. Takže tyto mezery klasické kinematiky budou považovány za absolutní, invariantní, jinými slovy ne závisí na přechodu z jednoho referenčního rámce na jiný. Zda relativistická kinematika. V tom mohou mezery v přechodu mezi referenčními rámečky se lišit. Bylo by správnější říci, že nemohou, ale měli by pravděpodobně. Z tohoto důvodu se simultánnost dvou náhodných událostí stává relativní a je předmětem zvláštního zvážení. Proto v relativistické kinematice jsou dvě pojmy - prostor a čas - spojeny do jednoho.

Kinematika bodu materiálu: rychlost, zrychlení a další veličiny

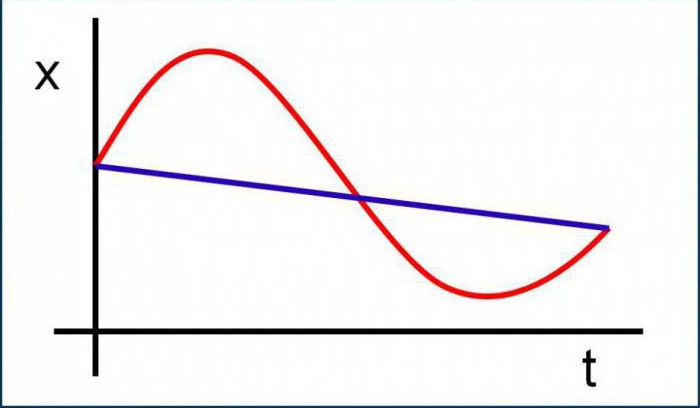
Pro pochopení této části alespoň trochufyziky, je třeba řídit se v nejzákladnějších koncepcích, znát definice a reprezentovat to, co konkrétní množství představuje obecně. Nic není komplikované, ve skutečnosti je vše velmi snadné a jednoduché. Pojďme zvážit, možná pro začátek, základní pojmy používané v problémech kinematiky.

Pohyb

Budeme považovat mechanický pohyb za proces,během něhož jeden nebo jiný idealizovaný objekt mění svou polohu v prostoru. Současně lze říci, že změna je relativní vůči ostatním tělům. Je také nutné vzít v úvahu skutečnost, že současně existuje určitý časový interval mezi oběma událostmi. Můžete například vybrat určitý interval, který vznikne během uplynulého času mezi tím, jak tělo přišlo z jedné pozice do druhé. Poznamenáváme také, že těla mohou a budou vzájemně spolupracovat podle obecných mechaniky. To je přesně to, co nejčastěji funguje kinematika určitého materiálu. Referenčním rámcem je následující koncept, který je s ním neodmyslitelně spojen.

Souřadnice

Mohou být nazývány běžnými daty, cožumožňují určit pozici těla najednou nebo jinou. Souřadnice jsou neoddělitelně spjaty s pojmem referenčního systému, stejně jako se sítí. Nejčastěji kombinace písmen a čísel.

Radiální vektor

Z názvu by mělo být jasné, že onje sám o sobě. Nicméně o tom budeme podrobněji diskutovat. Pokud se bod pohybuje po určité trajektorii a my přesně víme původ jednoho nebo jiného referenčního systému, můžeme kdykoli nakreslit vektor rádiusu. Připojí počáteční polohu bodu s okamžitým nebo konečným bodem.

Trajektorie

Bude nazývána spojitá čára, která je položena jako výsledek pohybu materiálu v určitém referenčním rámci.

Rychlost (lineární i úhlová)

To je hodnota, která vám může říci, jak rychle tělo projde tímto nebo tím vzdáleným intervalem.

Zrychlení (jak úhlové, tak lineární)

Zobrazuje, podle jakého zákona a jak rychle se změní parametr rychlosti těla.

Možná, tady jsou - základní prvky kinematikymateriální bod. Mělo by být poznamenáno, že jak rychlost, tak zrychlení jsou vektorová veličina. A to znamená, že nemají jen orientační hodnotu, ale také určitý směr. Mimochodem, mohou být nasměrovány jak v jednom směru, tak naopak. V prvním případě se tělo urychlí, v druhém brzdí.

Nejjednodušší úkoly

Kinematika bodu materiálu (rychlost,zrychlení a vzdálenost, ve kterých jsou prakticky zásadní koncepty) ani nepředstavuje velký počet úkolů, ale mnoho z jejich různých kategorií. Pokusíme se vyřešit poměrně jednoduchý problém, abychom zjistili vzdálenost, kterou tělo cestovalo.

Předpokládejme, že podmínky, které máme k dispozici,následující. Auto jezdec stojí na startovní čáře. Provozovatel vydá signál s vlajkou a vůz se náhle rozbije. Zjistěte, zda bude moci v soutěži závodníků nastavit nový rekord, pokud bude vzdálenost rovnající se sto metrů, další vůdce prošel za 7,8 sekundy. Zrychlete auto tak, aby se rovnalo 3 metry, dělené sekundou na čtverec.

Tak, jak vyřešit tento problém? Je to docela zajímavé, protože nevyžadujeme "suchou" definici určitých parametrů. Je to rozjasněné otočením a jistou situací, která diverzifikuje proces řešení a hledání indikátorů. Ale co bychom měli být vedeni dříve, než se k tomuto úkolu dostaneme?

1. Kinematika věcného bodu zahrnuje použití v tomto případě zrychlení.

2. Řešení je navrženo pomocí vzorce vzdálenosti, protože jeho číselná hodnota se objevuje v podmínkách.

Problém je řešen jednoduše. Pro tento účel použijeme vzorec vzdálenosti: S = VoT + (-) AT ^ 2/2. Jaký je význam? Musíme zjistit, jak dlouho bude jezdec projet přes stanovenou vzdálenost, a pak porovnat skóre s rekordem, aby zjistil, zda ho porazí nebo ne. Pro tento účel zvolíme čas, získáme vzorec pro něj: AT ^ 2 + 2VoT - 2S. To není nic než kvadratická rovnice. Ale auto se rozbije, což znamená, že počáteční rychlost bude 0. Při řešení rovnice se diskriminaci rovná 2400. Chcete-li najít čas, musíte extrahovat kořen. Udělejme na druhé desetinné místo: 48,98. Najděme kořen rovnice: 48.98 / 6 = 8.16 sekund. Ukazuje se, že jezdec nemůže porazit stávající záznam.